Resources for QCE Senior School Psychology

Research Design

Which research design and statistical test?

Correlational

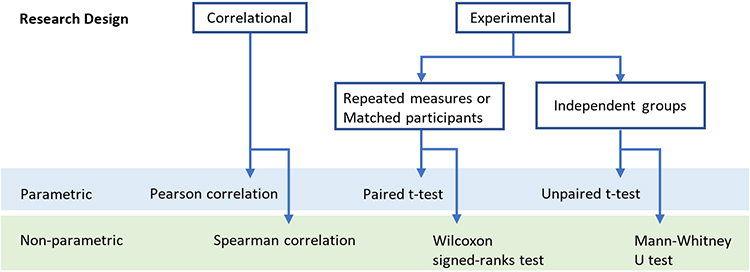
Correlational designs are used to test whether there is a relationship between two measures. e.g. Is there a relationship between a person’s age and their IQ? Positive correlation would mean that IQ increases with age. Negative correlation would indication that IQ decreases with age. No significant correlation (the null hypothesis) is that there is no significant relationship, i.e. a person’s IQ is not related to their age. Correlational designs have no independent or dependent variables, and only test for the linear relationship between two measures.

Experimental

Experimental designs are used to test whether there is a significant difference between two (or more) groups or between measures at different times or under different conditions (e.g. experimental versus control groups/conditions). The alternate hypothesis is that the two groups/conditions are different. The null hypothesis is that the two groups/conditions are not different. Experimental designs have an independent variable that is the group/condition that is controlled by the experimenter and a dependent variable that is the measure assessed. Experimental designs test the effect of the independent variable on the dependent variable.

Experimental designs can use either:

Independent Groups: Two (or more) independent groups of participants are compared. e.g. Is IQ different in girls compared with boys? The independent variable is gender that is controlled in the experiment, i.e. the experimenter selects participants and assigns them to groups according to their gender (girls versus boys). The dependent variable is IQ that is measured by the experimenter. The experimental design tests the effect of gender on IQ. The null hypothesis is that IQ will not be different between girls and boys. The alternate hypothesis is that IQ will be different between girls and boys, either greater for girls compared with boys or lower for girls compared with boys. As groups are independent, there can be a different number of participants in each group.

Matched Participants: Two (or more) groups of participants are compared, but participants between groups are matched one-to-one on other relevant factors, to control potential effects of other factors that might influence results. e.g. Is IQ different in girls compared with boys, controlling for potential effects of age? The independent variable is gender that is controlled in the experiment, but the experimenter selects a pairs of participants, one girl and one boy, of exactly the same age, paired one-to-one between the two participant groups. The dependent variable is IQ that is measured by the experimenter. The null hypothesis is that IQ will not be different between girls and boys. The alternate hypothesis is that IQ will be different between girls and boys. Any difference in IQ observed between girls and boys cannot be influenced by age as the two groups are exactly matched in age. As groups are matched one-to-one, there must be the same number of participants in each group.

Repeated Measures: Two (or more) measures taken from the same participants under different conditions or at different times are compared. e.g. Is IQ different when measured at the start of the school day compared with the end of the school day? The independent variable is the time of day that is controlled in the experiment, i.e. the experimenter selects the times of day to measure IQ and compare. The dependent variable is IQ that is measured by the experimenter. The dependent variable is measured in all participants at both times of day (i.e. repeated measures) and compared. The experimental design tests the effect of the time of day of the IQ test on the measured IQ. The null hypothesis is that there will be no difference in IQ measured at the start compared with the end of the school day. The alternate hypothesis is that measured IQ will be different at the start compared with the end of the school day, either greater at the start of the day compared with the end or less at the start of the day compared with the end. As measures are repeated under both conditions in all participants, there must be an equal number of measures (i.e. equal participants) in each condition.